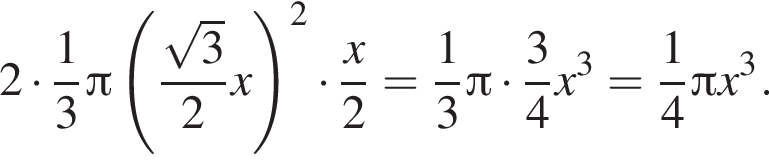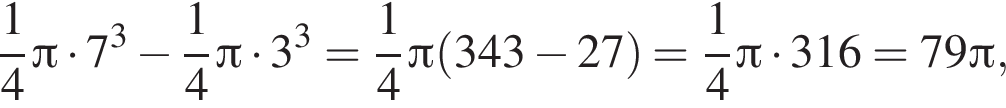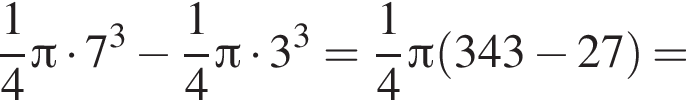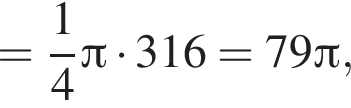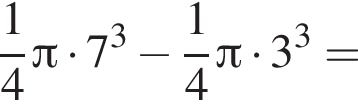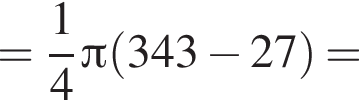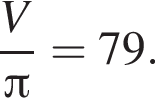Укажите номер рисунка, на котором изображен равнобедренный треугольник.
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 210°. Найдите градусную меру меньшего угла.
Результат разложения многочлена x (4a − b) + b − 4a на множители имеет вид:
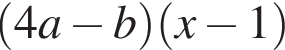
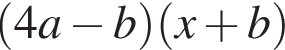
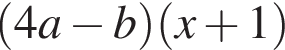
Точка С делит отрезок АВ в отношении 5 : 3, считая от точки А. Если длина отрезка АВ равна 24, то длина отрезка СВ равна:
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см. рис.). Длина диагонали AC параллелограмма равна:
Образующая конуса равна 26 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.
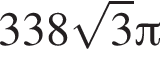

Среди данных чисел укажите номера четных чисел, если известно, что число а — нечетное.
| 1) 8 · a; | 2) 11 · a | 3) a + 6 | 4) a2 | 5) a + 13 |
Значение выражения 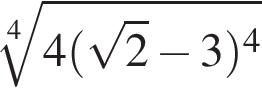 равно:
равно:
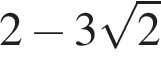
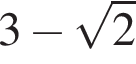
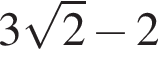
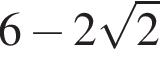
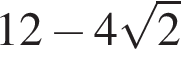
Точки A(-3;3) и B(4;1) — вершины квадрата ABCD. Периметр квадрата равен:
Найдите произведение координат точки пересечения прямых 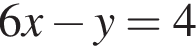 и
и 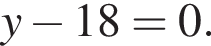
Укажите номера функций, которые являются четными.
| 1) y = 0,2x2; | 2) 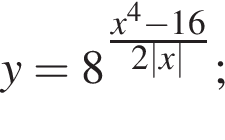 | 3) 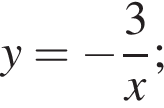 | 4) 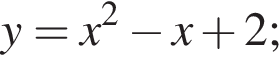 | 5)  |
Сократите дробь 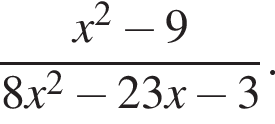
Упростите выражение
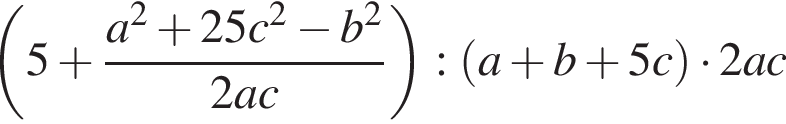
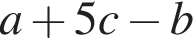
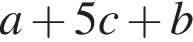
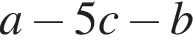
На координатной плоскости изображен тупоугольный треугольник ABC с вершинами в узлах сетки (см. рис.). Косинус угла ABC этого треугольника равен:
Площадь боковой поверхности цилиндра равна ![]() и его объем равен
и его объем равен ![]() Найдите высоту цилиндра.
Найдите высоту цилиндра.
Если 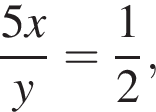 то значение выражения
то значение выражения 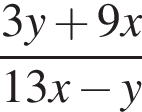 равно:
равно:
Корень уравнения
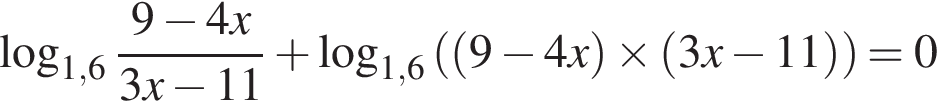
(или сумма корней, если их несколько) принадлежит промежутку:
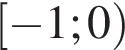
На круговой диаграмме представлена информация о продаже 200 кг овощей в течение дня. Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
А) Масса (в килограммах) проданной капусты равна ...
Б) Отношение, выраженное в процентах, которое показывает, на сколько масса проданного картофеля меньше массы проданных помидоров, равно ...
В) Отношение, выраженное в процентах, которое показывает, на сколько масса проданной свеклы больше массы проданного лука, равно ...
1) 25
2) 40
3) 4
4) 125
5) 38
6) 19
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
| Начало предложения | Окончание предложения | |
| А) Значение выражения Б) Значение выражения В) Значение выражения | 1) 2) 3) 4) 2,5 5) 6) 5 |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения, если известно, что две перпендикулярные плоскости
![]() и
и ![]() пересекаются по прямой a и точка A принадлежит плоскости
пересекаются по прямой a и точка A принадлежит плоскости ![]() (см. рис.).
(см. рис.).
1. Любая прямая, проходящая через точку A и пересекающая плоскость ![]() пересекает прямую a.
пересекает прямую a.
2. Существует единственная прямая, проходящая через точку A и перпендикулярная плоскости ![]()
3. Прямая, проходящая через точку A и перпендикулярная плоскости ![]() перпендикулярна плоскости
перпендикулярна плоскости ![]()
4. Любая точка прямой a лежит в плоскостях ![]() и
и ![]()
5. Любая прямая, лежащая в плоскости ![]() и перпендикулярная прямой a, перпендикулярна плоскости
и перпендикулярная прямой a, перпендикулярна плоскости ![]()
6. Любая прямая, перпендикулярная прямой a, принадлежит плоскости ![]()
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Найдите произведение корней (корень, если он единственный) уравнения 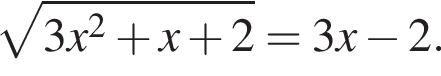
Найдите значение выражения 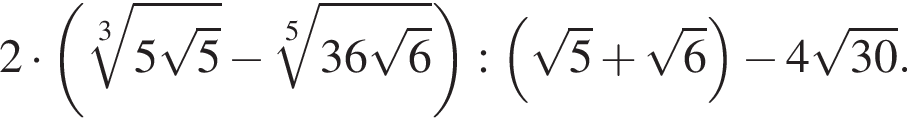
Точки N и М лежат на сторонах АВ и AD параллелограмма ABCD так, что AN : NB = 1 : 2, AM : MD = 1 : 2. Площадь треугольника CMN равна 45. Найдите площадь параллелограмма ABCD.
Найдите сумму целых решений неравенства 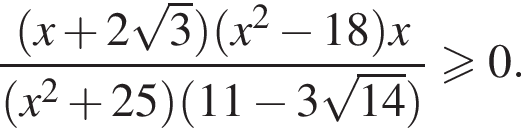
Найдите сумму всех целых решений неравенства 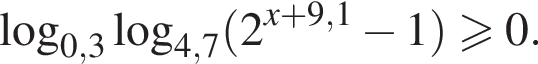
Если ![]() и
и ![]() — корни уравнения
— корни уравнения 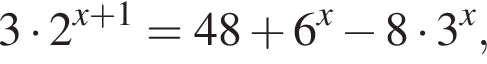 то значение
то значение ![]() равно ... .
равно ... .
В прямоугольнике ABCD выбраны точки L на стороне BC и M на стороне AD так, что ALCM — ромб. Найдите площадь этого ромба, если AB = 3, BC = 9.
По прямым параллельным путям равномерно в противоположных направлениях движутся два поезда: по первому пути — скорый поезд со скоростью 108 км/ч, по второму — пассажирский со скоростью 68,4 км/ч. По одну сторону от путей на расстоянии 100 м от первого пути и 20 м от второго растет дерево. Если пренебречь шириной пути, то в течение скольких секунд t пассажирский поезд, имеющий длину 165 м, будет загораживать дерево от пассажира скорого поезда? В ответ запишите значение выражения 15t.
Объем правильной треугольной пирамиды SABC равен 13. Через сторону основания ВС проведено сечение, делящее пополам двугранный угол SBCA и пересекающее боковое ребро SA в точке М. Объем пирамиды МАВС равен 6. Найдите значение выражения ![]() где
где ![]() — угол между плоскостью основания и плоскостью боковой грани пирамиды SABC.
— угол между плоскостью основания и плоскостью боковой грани пирамиды SABC.
Отрезок BD является биссектрисой треугольника АВС, в котором 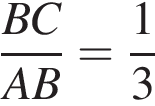 и
и 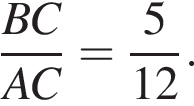 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
Равнобедренная трапеция с основаниями длиной 7 и 3 и острым углом 60° вращается вокруг прямой, содержащей ее боковую сторону. Найдите объем тела вращения V и в ответ запишите значение выражения ![]()

 — все углы разные.
— все углы разные. — все углы разные.
— все углы разные. — треугольник равнобедренный.
— треугольник равнобедренный. — все углы разные.
— все углы разные. — все углы разные.
— все углы разные. равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
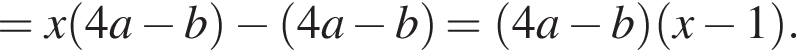

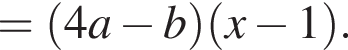
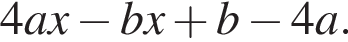
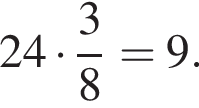
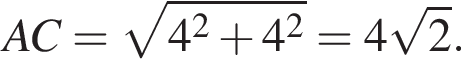
 где r — радиус основания, l — образующая. Найдем радиус:
где r — радиус основания, l — образующая. Найдем радиус:  Таким образом, площадь боковой поверхности равна:
Таким образом, площадь боковой поверхности равна: 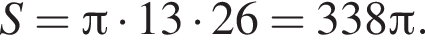
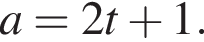 Тогда имеем:
Тогда имеем: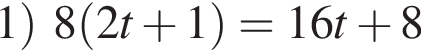 — четное;
— четное;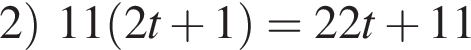 — нечетное;
— нечетное; — нечетное;
— нечетное; — нечетное;
— нечетное;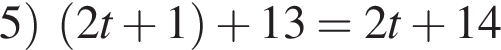 — четное.
— четное.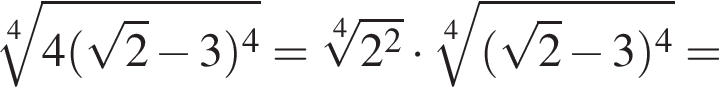
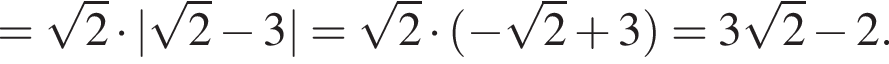

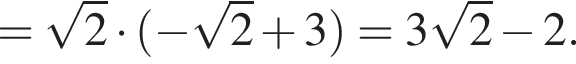
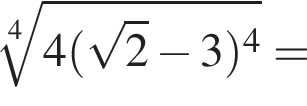
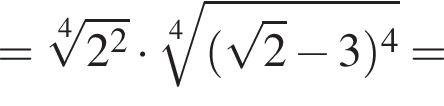

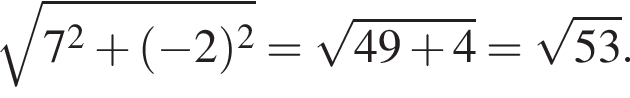 Таким образом, периметр квадрата равен:
Таким образом, периметр квадрата равен: 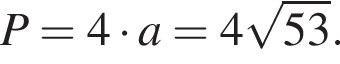
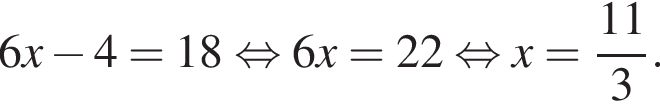
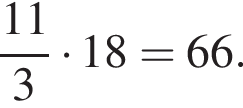
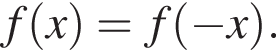 Проверим каждую функцию:
Проверим каждую функцию: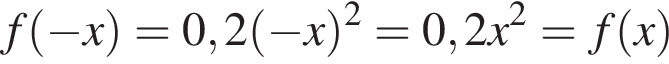 — чётная функция;
— чётная функция;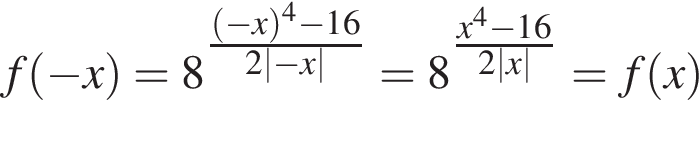 — чётная функция;
— чётная функция;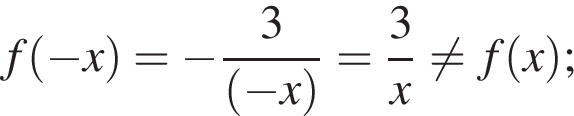
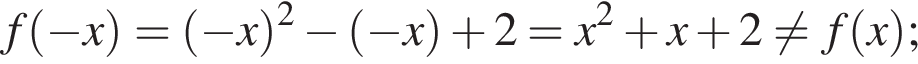
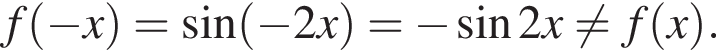
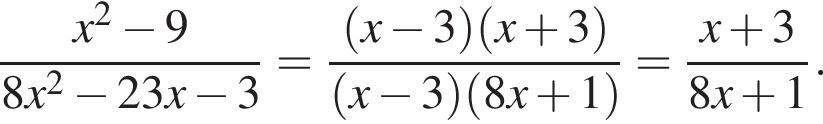
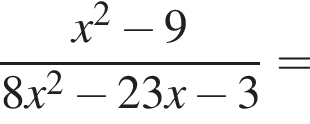
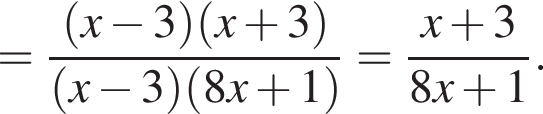
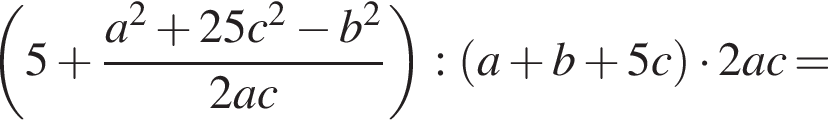
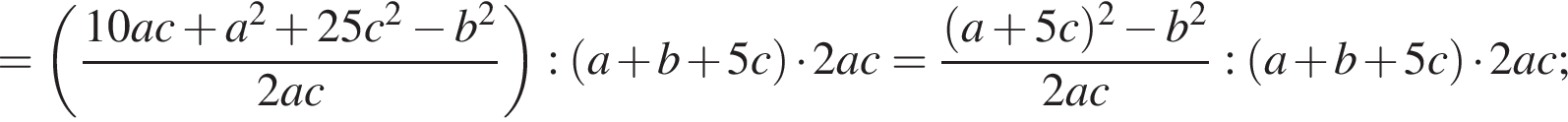
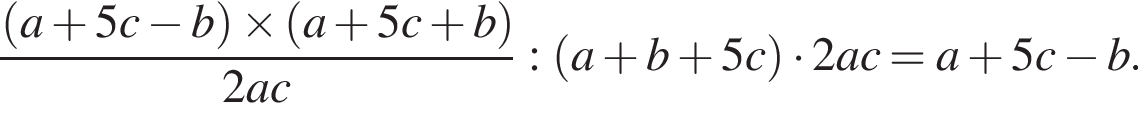
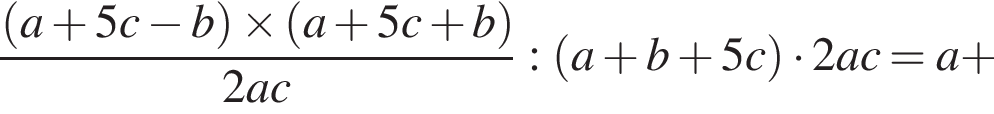
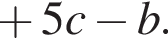

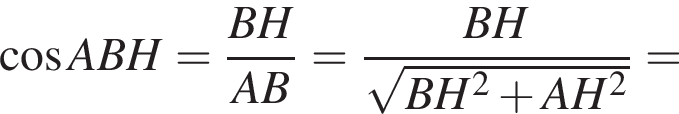
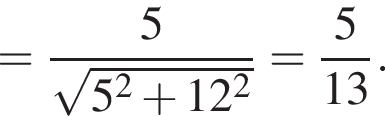
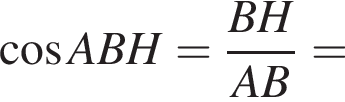
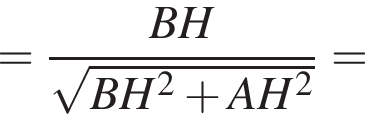
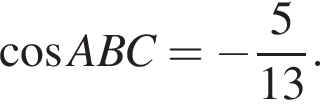
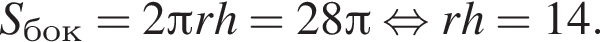
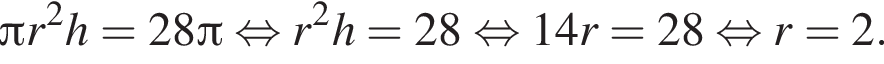


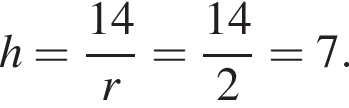
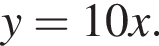 Тогда получим:
Тогда получим: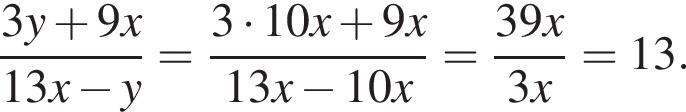
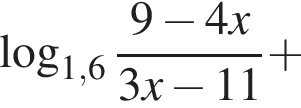
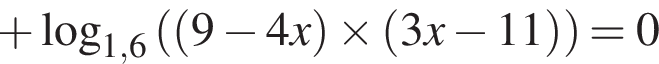
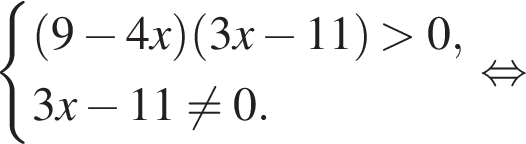
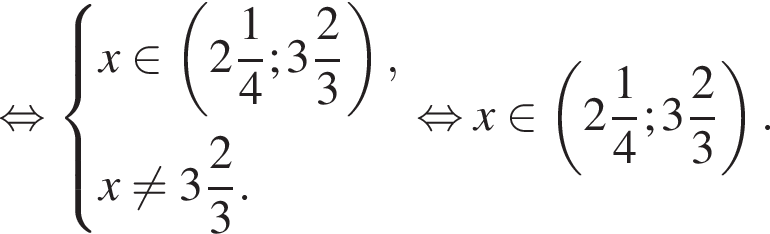
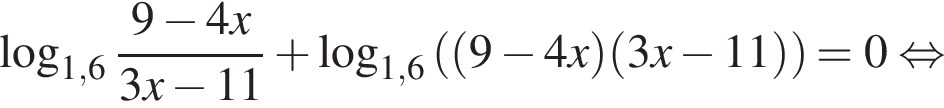
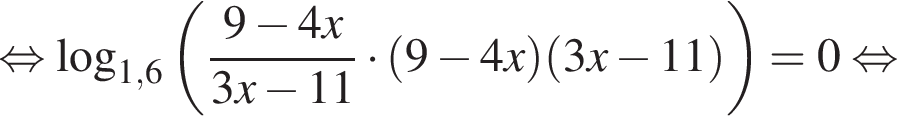
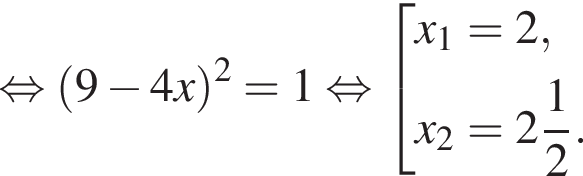
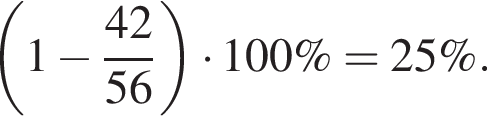
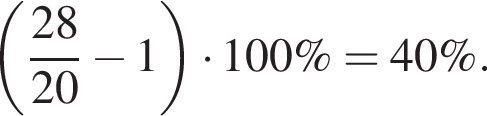
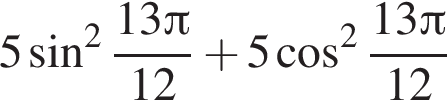 равно ...
равно ...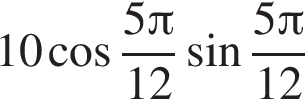 равно ...
равно ...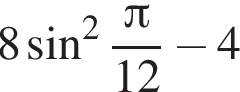 равно ...
равно ...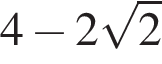
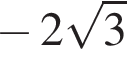
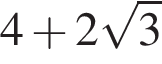
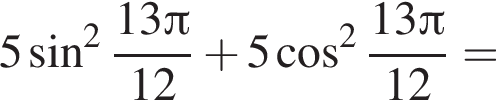
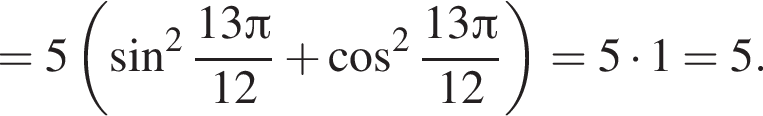
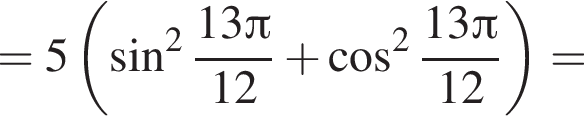
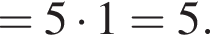
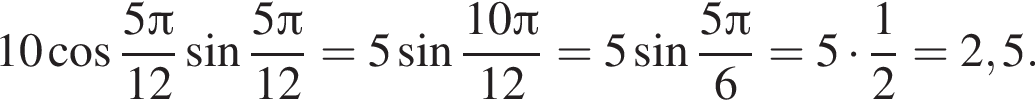

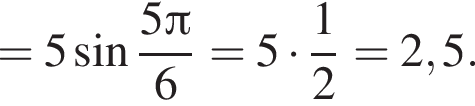
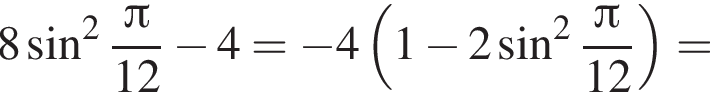
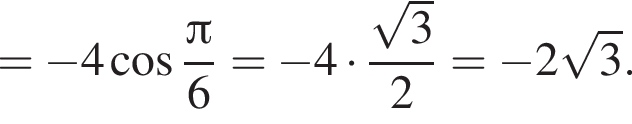
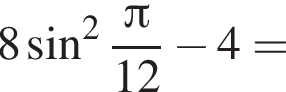
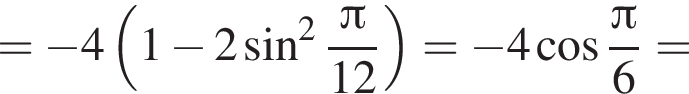
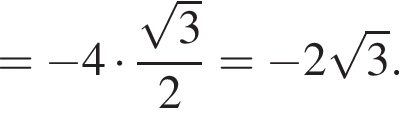
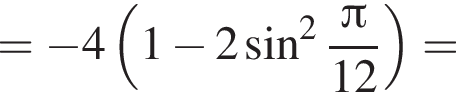
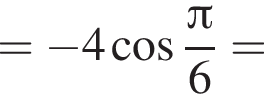
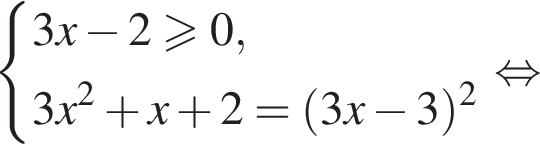
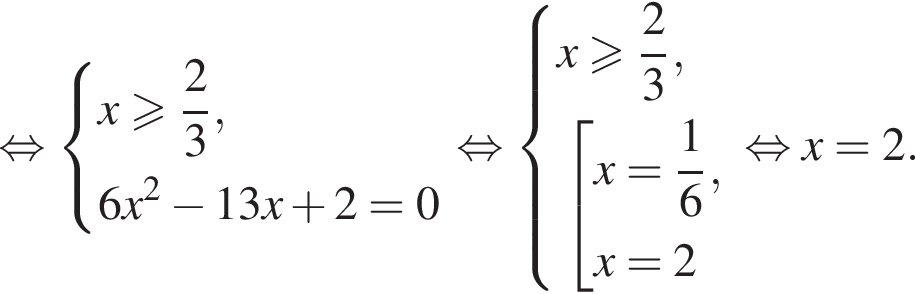
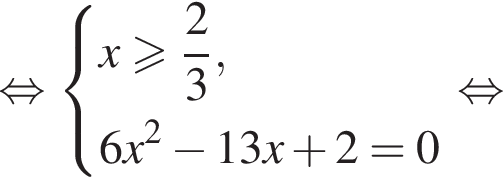
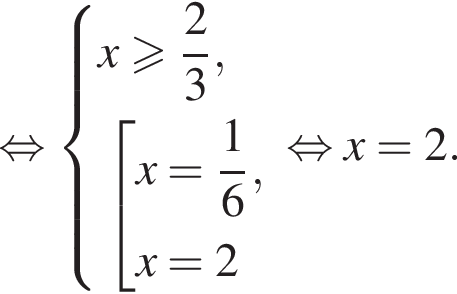
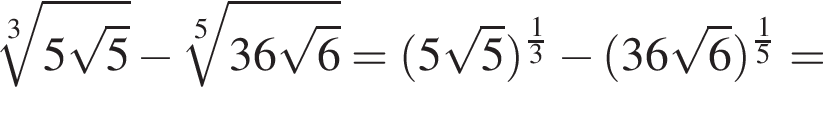
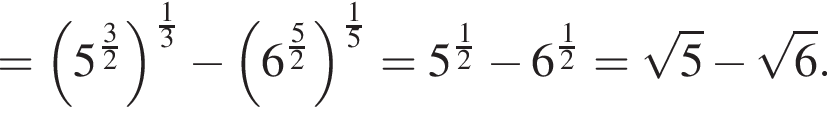
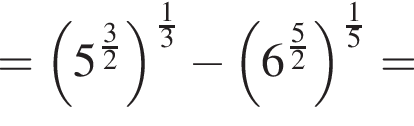
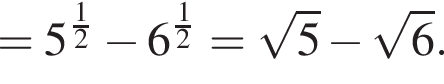
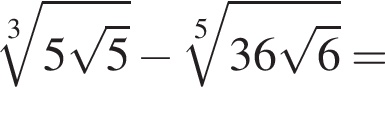
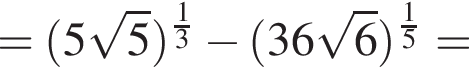
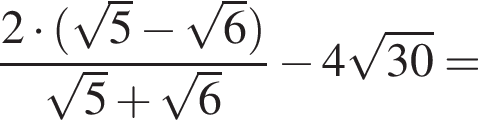
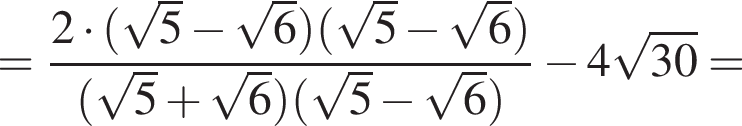
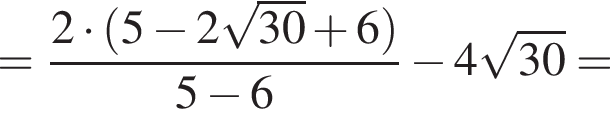
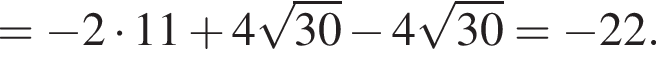

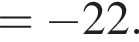
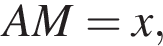 тогда
тогда 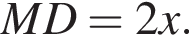 Аналогично
Аналогично 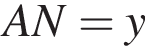 и
и  Площадь параллелограмма представим в виде суммы площадей треугольников, из которых он составлен:
Площадь параллелограмма представим в виде суммы площадей треугольников, из которых он составлен:

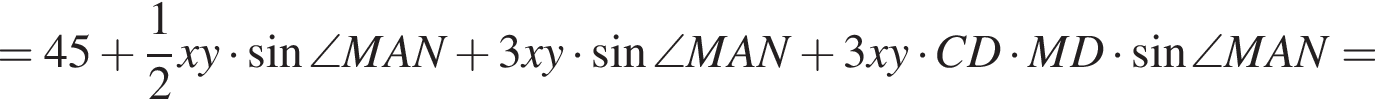
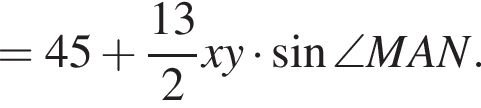
 так как
так как 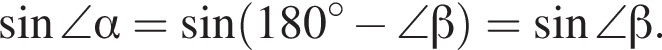 Площадь параллелограмма равна
Площадь параллелограмма равна 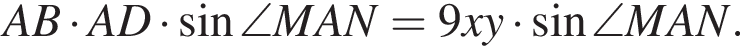 Имеем:
Имеем: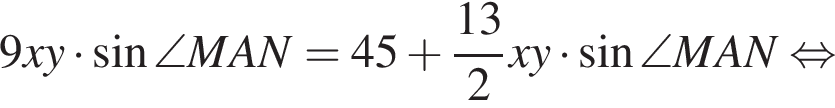
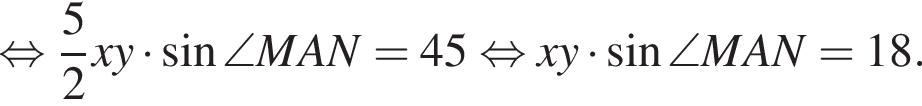
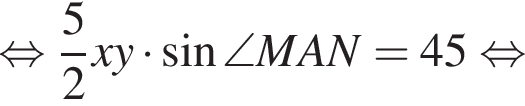

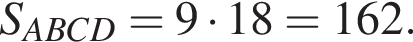
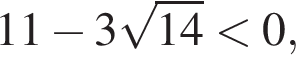 поскольку
поскольку 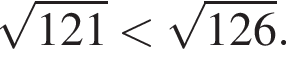 Число,
Число, 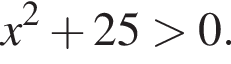 Домножим неравенство на эти числа, поменяв знак, и решим его.
Домножим неравенство на эти числа, поменяв знак, и решим его.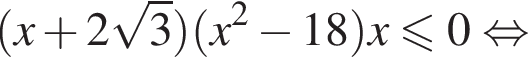
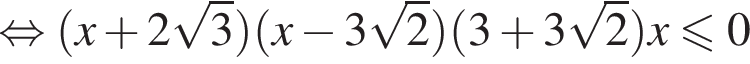
 Целыми решениями неравенства являются числа −4, 0, 1, 2, 3, 4, их сумма равна 6.
Целыми решениями неравенства являются числа −4, 0, 1, 2, 3, 4, их сумма равна 6.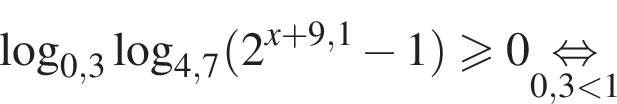
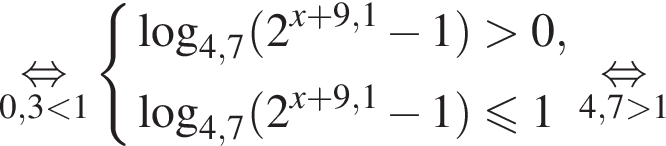
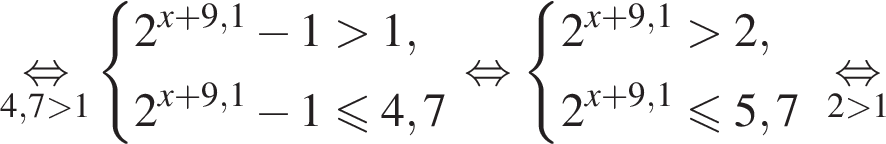
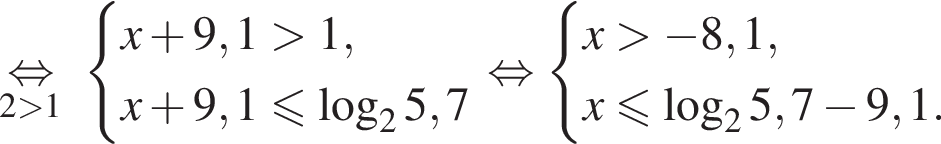
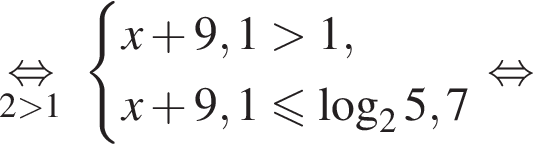
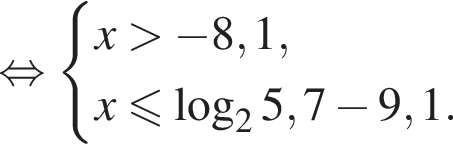
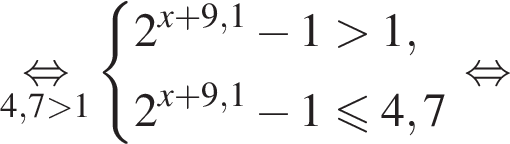
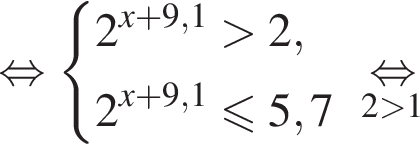
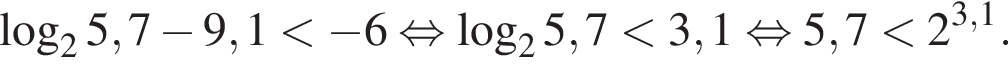
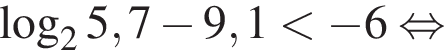
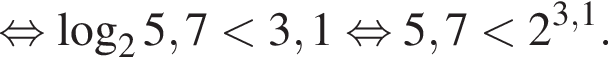

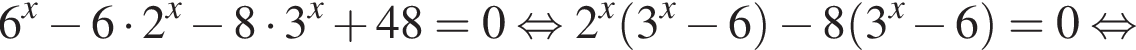
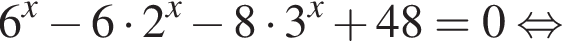
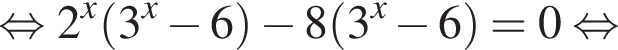
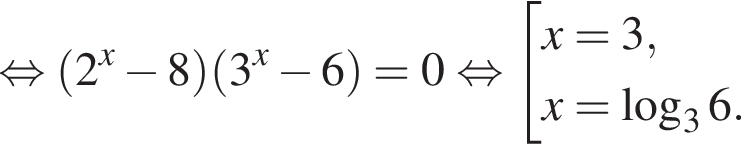
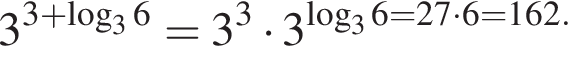
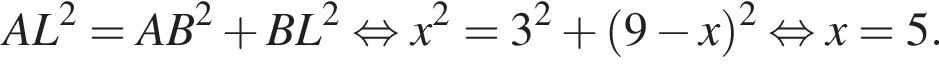
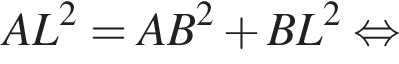
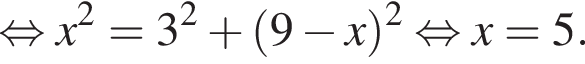
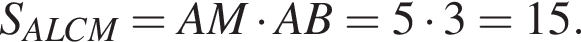

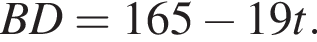 Тогда:
Тогда: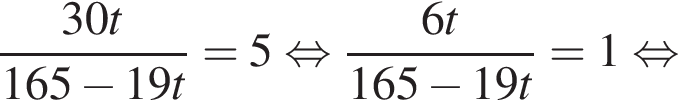
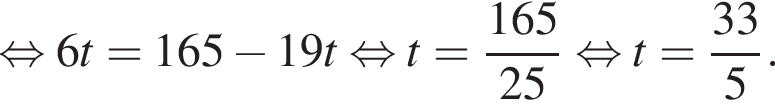

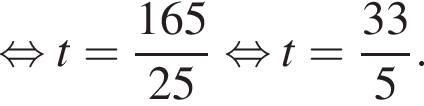
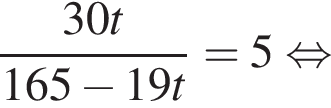
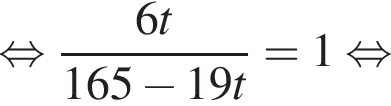
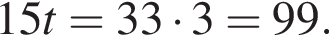
 откуда
откуда 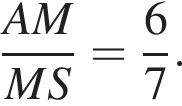 Точка O — центр окружности, вписанной в треугольник ABC, в нее проецируется высота SO. Пусть сторона основания пирамиды равна a, тогда высота
Точка O — центр окружности, вписанной в треугольник ABC, в нее проецируется высота SO. Пусть сторона основания пирамиды равна a, тогда высота 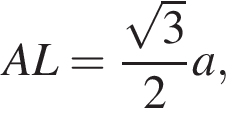
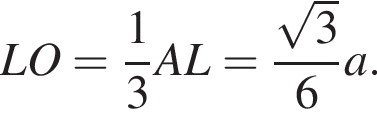 Из свойства биссектрисы в треугольнике SLA:
Из свойства биссектрисы в треугольнике SLA: 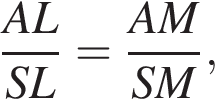
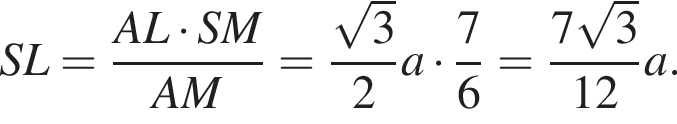
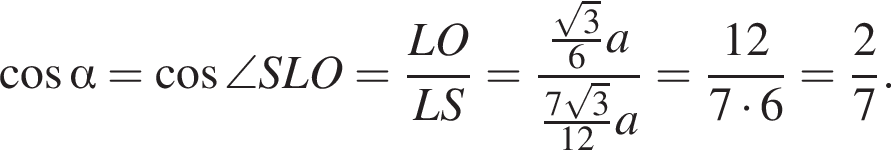
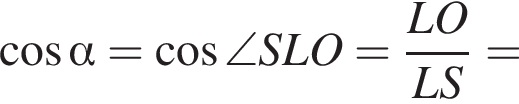
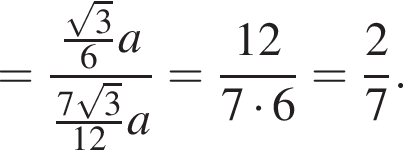
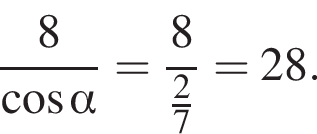
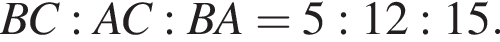 По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 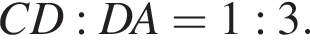 Значит, если
Значит, если  то
то 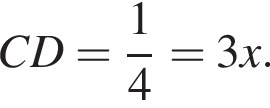
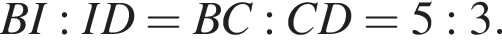 Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что 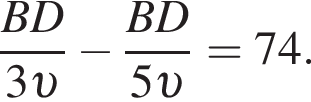
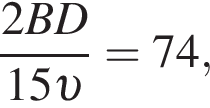 откуда
откуда 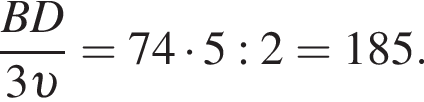
 и потому объем двух таких конусов равен
и потому объем двух таких конусов равен